DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Sources et applications

DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Sources et applications

On se propose de décrire très sommairement quelques types classiques d’équations aux dérivées partielles issues principalement de la physique et de préciser leurs interventions dans des domaines variés des mathématiques.

Alors que les solutions des équations différentielles ordinaires dépendent d’une ou de plusieurs constantes arbitraires, celles des équations et systèmes d’équations aux dérivées partielles dépendent de fonctions arbitraires; il y a donc des familles beaucoup plus riches de solutions. Ce fait se voit sur l’exemple particulièrement simple d’une équation linéaire du premier ordre:

on lui associe le système différentiel des caractéristiques :

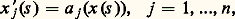dont les trajectoires sont les courbes caractéristiques de l’équation. L’équation aux dérivées partielles équivaut alors à une équation différentielle ordinaire sur chaque courbe caractéristique. Posant:

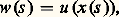cette équation différentielle s’écrit:

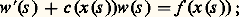il faut la compléter par une donnée initiale sur chaque caractéristique, ce qui introduit une fonction arbitraire. On remarquera sur cet exemple qu’une solution d’une équation sans second membre (f = 0) ne peut s’annuler en un point sans s’annuler sur toute la courbe caractéristique qui passe par ce point.

La façon la plus courante de déterminer une solution, en particulier dans les problèmes d’origine physique, est de fixer les valeurs de la fonction et d’une ou plusieurs de ses dérivées sur des hypersurfaces. On dit que le problème est bien posé lorsque cela détermine une solution et une seule. Pour traduire une situation physique, un problème doit non seulement être bien posé au sens précédent, mais posséder en plus une propriété de stabilité: la solution doit dépendre continûment des données (en un sens à préciser dans chaque problème particulier). Cette condition est automatiquement vérifiée dans les problèmes linéaires (c’est une conséquence du théorème du graphe fermé; cf. espaces VECTORIELS TOPOLOGIQUES).

Il est remarquable, ce qui sera évident ci-dessous, que les premiers travaux systématiques ont porté sur des équations du second ordre, qui se sont présentées en mécanique, puis dans la théorie de la chaleur. L’étude des équations du premier ordre, la plus simple du point de vue mathématique, n’est venue que plus tard.

1. L’équation des ondes et le type hyperbolique

L’équation des ondes (équation de d’Alembert):

régit le comportement de la densité dans une onde sonore, c’est-à-dire une perturbation de faible amplitude d’un gaz non visqueux au repos. Dans une série de phénomènes physiques représentés par des grandeurs vectorielles, chaque composante des vecteurs concernés obéit à cette même équation: ondes transversale et longitudinale dans un solide élastique ^{[cf. ONDES (physique)]}, ondes électromagnétiques ^{[cf. ÉLECTRICITÉ]}, etc. Il faut y ajouter les phénomènes analogues dépendant seulement d’une ou deux variables d’espace; parmi eux, les vibrations transversales d’un fil élastique donnent lieu au cas particulier de l’équation des cordes vibrantes:

la plus ancienne à avoir été explicitement étudiée (dans la décennie de 1740 par d’Alembert, Daniel Bernoulli et Euler).

La possibilité d’écrire toutes les solutions de l’équation des cordes vibrantes sous la forme: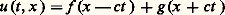

permet d’en voir facilement certaines propriétés:

a ) Le problème de Cauchy est bien posé, tant dans le futur (t 礪 t ⁰) que dans le passé (t 麗 t ⁰). Ce problème s’énonce ici: «Trouver u vérifiant l’équation (2) et de plus les conditions:

où u ⁰ et u ¹ sont des fonctions données.»

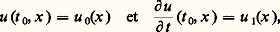b ) Les solutions se propagent à la vitesse c. Cette affirmation délibérément vague peut se préciser de plusieurs façons. Par exemple en revenant au problème de Cauchy, avec t ⁰ nul pour simplifier, si u ⁰ et u ¹ s’annulent en dehors d’un intervalle [a , b ], u (t , x ) s’annule lorsque x est en dehors de l’intervalle [a 漣 c |t |, b + c |t |] (fig. 1). Sur cette figure, si les données de Cauchy u (0, x ) et 煉u / 煉t (0, x ) s’annulent en dehors de [a , b ], la solution u s’annule sur toute la région ombrée.

Cette propriété peut s’exprimer de façon équivalente en termes de domaines de dépendance : u (t , x ) ne dépend que des restrictions de u ⁰ et u ¹ à l’intervalle [x 漣 c |t |, x + c |t |] (fig. 1). Le domaine de dépendance du point P est le segment renforcé sur l’axe des x ; on peut calculer u (P) à l’aide des données de Cauchy sur ce segment.

c ) Les singularités de la solution se propagent, elles aussi, à la vitesse c . Si par exemple u ¹ présente une discontinuité au point x ⁰, on retrouvera des discontinuités des dérivées premières de u aux points (t , x 漣 ct ) et (t , x + ct ).

La possibilité d’expliciter toutes les solutions sous une forme simple est tout à fait spéciale à l’équation des cordes vibrantes. Mais les propriétés que nous en avons tirées se démontrent par d’autres méthodes pour toute une classe d’équations et de systèmes qu’on appelle hyperboliques. C’est dans cette classe qu’on trouve les équations de base auxquelles obéissent les phénomènes physiques réversibles, à commencer par l’équation des ondes. La formulation du problème de Cauchy n’a pas besoin d’être changée, du moins tant qu’on se limite à une équation du second ordre. La géométrie de la propagation devient plus compliquée et, pour la décrire dans le cas général, même linéaire, il faut recourir aux courbes bicaractéristiques dont on trouvera la définition au début de l’article équations aux DÉRIVÉES PARTIELLES - ANAlyse microlocale. Nous allons décrire ici deux résultats simples sur l’équation:

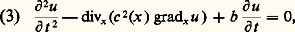équation qui décrit la propagation d’une onde amortie avec une vitesse dépendant du point où on se trouve (comme le son dans une atmosphère inhomogène). Nous poserons:

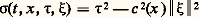(c’est ce qu’on appelle le symbole principal ).

Soit u une solution de (3) qui s’annule d’un côté d’une hypersurface d’équation: S(t , x ) = 0. On peut démontrer que si u ne s’annule pas sur tout un voisinage de , S vérifie l’équation aux dérivées partielles non linéaire du premier ordre:

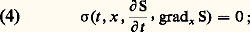on dit que c’est une hypersurface caractéristique .

Supposons de plus que u soit deux fois continûment dérivable en dehors de mais discontinue sur . Nous noterons [u ] sa discontinuité; [u ] est donc définie sur comme limite de u (x ) quand x tend vers un point de en restant du côté où u ne s’annule pas identiquement. Si on cherche alors à écrire l’équation (3) au sens des distributions, on voit apparaître une double couche portée par de densité [u ] que multiplie le premier membre de (4), ce qui donne la démonstration dans ce cas particulier. Il apparaît également une simple couche dont la densité est à un coefficient non nul près:

où h est une fonction qui se calcule à partir des coefficients de (3) et de S. On voit donc que la discontinuité [u ] vérifie une équation linéaire du premier ordre dont le système caractéristique est:

les trajectoires de ce système qui ont un point sur sont tout entières sur cette hypersurface du fait qu’elle est caractéristique, ce sont des courbes bicaractéristiques de l’équation (3).

Le point important est que u vérifie une équation différentielle le long de chacune de ces bicaractéristiques, d’où il résulte que sa valeur en un point la détermine sur toute la bicaractéristique issue de ce point. C’est en ce sens que la discontinuité se propage le long des bicaractéristiques. De même, si à l’instant t = 0 la discontinuité présente un pic au voisinage de x ⁰, ce pic se retrouvera en chaque point de la bicaractéristique issue de (0, x ⁰). On notera la nature cinématique des bicaractéristiques: elles représentent des points qui se déplacent à la vitesse c perpendiculairement aux surfaces S = C ^te ; on retrouve ainsi le comportement des rayons lumineux.

Pour achever de se ramener à la définition générale des bicaractéristiques telle qu’elle sera donnée au début de l’article équations aux DÉRIVÉES PARTIELLES - ANALYSE MICROlocale, on vérifiera que, si on pose:

on a sur les bicaractéristiques: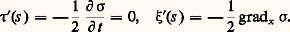

Il est remarquable que les conclusions de l’étude que nous venons de présenter aient été dégagées par Huygens dans son Traité de la lumière (écrit en 1678 et publié en 1690) sur la base de considérations physiques et géométriques avant que qui que ce soit n’ait écrit une équation aux dérivées partielles (cf. fig. 2).

Une méthode importante est l’approximation des hautes fréquences qui repose sur la construction de solutions approchées de la forme exp (i 益﨏) v, où v possède un développement limité en 益 au voisinage de l’infini. On trouve que 﨏 vérifie encore l’équation des caractéristiques (4) et que chaque terme du développement limité de v vérifie une équation linéaire du premier ordre dont les courbes caractéristiques sont des bicaractéristiques de l’équation étudiée. On arrive à donner une base mathématique rigoureuse aux calculs qui se faisaient en optique, dans l’étude des radars, etc.

Une série de problèmes importants dans les applications concernent la diffusion («scattering»): c’est l’étude du rapport entre les comportements asymptotiques des solutions pour t tendant vers moins et plus l’infini.

On appelle systèmes d’évolution du premier ordre symétriques, ceux qui ont la forme:

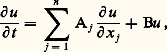où u est la fonction inconnue (vectorielle) et les A^j des matrices autoadjointes. Ce sont des systèmes hyperboliques et, en fait, la plupart des systèmes les plus importants peuvent se mettre sous cette forme.

L’équation de Dirac, qui décrit l’évolution d’une particule relativiste de spin ½, est un tel système, où la fonction d’onde de la particule a quatre composantes. L’équation des ondes peut elle aussi se mettre sous la forme d’un système symétrique. Pour cela, on prend pour fonctions inconnues:

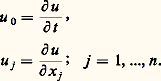L’équation des ondes devient alors:

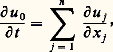et on complète le système en écrivant les équations qui expriment que les dérivations par rapport aux x ^j et à t commutent:

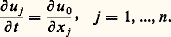Le sytème obtenu est bien symétrique.

D’autres équations que les hyperboliques ont des solutions qui se propagent, on en verra des exemples – tous non linéaires – dans l’article équations aux DÉRIVÉES PARTIELLES - ÉQUATIONS AUX DÉRIVÉES PARTIELLES NON LINÉAIRES. Mais, dans ces autres équations, la vitesse de propagation dépend toujours de la solution considérée.

2. Le type elliptique

L’équation de Laplace, ou de Poisson

Si dans l’équation des ondes on s’intéresse à des solutions stationnaires (c’est-à-dire indépendantes du temps), on tombe sur l’équation de Poisson:

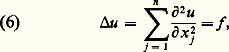plus connue sous le nom d’équation de Laplace lorsque le second membre est nul, et prototype des équations elliptiques. De même, si on s’intéresse aux solutions qui ne dépendent du temps que par un facteur e ⁱ size=1^諸t ou cos 諸(t 漣 t ⁰), on voit qu’elles vérifient l’équation de Helmholtz:

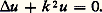Cette équation a des propriétés tout à fait analogues à celle de Laplace.

On retrouve l’équation de Laplace (à deux variables indépendantes) comme conséquence des conditions de Cauchy-Riemann. Elle est donc vérifiée par la partie réelle et la partie imaginaire pure de toute fonction analytique d’une variable complexe. Ce fait a été la source de certains problèmes de la théorie des équations aux dérivées partielles (quelles sont les propriétés des fonctions analytiques qui peuvent être généralisées ici?). Il a aussi été la source de certaines applications dont la plus célèbre est la méthode de Joukovski (à une certaine approximation, le calcul d’un écoulement incompressible autour d’une aile se ramène à un problème de représentation conforme ^{[cf. AÉRODYNAMIQUE]}.

Les problèmes bien posés pour l’équation de Laplace concernent en général les solutions sur un ouvert borné 行 de Rⁿ dont nous noterons 臨 la frontière. Les deux plus usuels sont:

– Le problème de Dirichlet : «Trouver u vérifiant (6) sur 行 et dont la restriction à 臨 est donnée.»

– Le problème de Neumann : «Trouver u vérifiant (6) sur 行 et dont la dérivée normale sur 臨 est donnée.»

À vrai dire, ce dernier n’est pas tout à fait bien posé. D’abord il n’y a pas unicité puisqu’en ajoutant à une solution une constante, on retrouve une autre solution. D’autre part, pour qu’il y ait existence, les données doivent vérifier une condition que nous allons trouver en utilisant l’outil fondamental pour ce genre de questions, la formule de Green :

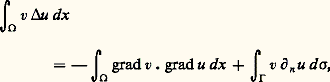où 煉ⁿ désigne la dérivée normale sortante et d 靖 la mesure superficielle; nous notons g la dérivée normale sortante (donnée) de u et nous appliquons la formule de Green avec v = 1, ce qui nous donne compte tenu de (6):

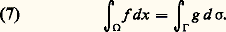Cette condition a une interprétation très claire dans tous les cas où 漣 grad u est le flux d’une grandeur (par exemple si 漣 u est le potentiel des vitesses d’un liquide animé d’un mouvement irrotationnel; ou si on est dans le cas stationnaire de l’équation de la chaleur, u est alors la densité d’énergie interne et 漣 grad u , moyennant un choix d’unités, son flux). Dans cette situation, le premier membre de (7) est la quantité de la grandeur en question créée à l’intérieur de 行 et le second membre la quantité qui sort à travers la frontière.

On rencontre très souvent des problèmes mêlés, c’est-à-dire où on donne u sur une partie de la frontière et sa dérivée normale sur le reste. Ces problèmes sont bien posés. Une série de problèmes généralisent celui de Neumann (condition de Newton, dérivées obliques...).

Les solutions des équations de Poisson et de Laplace et des équations analogues possèdent de multiples propriétés: elles sont analytiques, ne peuvent pas avoir de maximum ni de minimum à l’intérieur d’un domaine où l’équation est vérifiée. On appelle fonctions harmoniques les fonctions qui vérifient l’équation de Laplace ^{[cf. POTENTIEL ET FONCTIONS HARMONIQUES]}.

Applications à la topologie

Considérons une variété compacte V et munissons-la d’une métrique riemannienne, comme il est possible de le faire. On sait que cette métrique riemannienne induit pour tout k un produit scalaire sur l’espace vectoriel 廬^k des champs de formes extérieures de degré k sur V. La différentiation extérieure d qui opère de 廬^k dans 廬^k+1 possède donc un adjoint d . Posons:

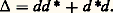Dans le cas des fonctions sur un espace euclidien, on retrouve bien le laplacien usuel; c’est essentiellement la formule:

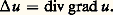Notons en général ^k la restriction de à 廬^k . On a alors le théorème de Hodge-de Rham : la dimension du noyau de ^k est le k -ième nombre de Betti de V.

Ce théorème a reçu une série de généralisations dont le célèbre théorème de l’indice d’Atiyah-Singer et, tout récemment, le résultat d’Alain Connes classifiant les feuilletages en attachant un indice aux opérateurs elliptiques sur chaque feuillet.

Principe des travaux virtuels et formulations variationnelles

Les équations vérifiées par le déplacement d’un solide élastique en équilibre forment un système elliptique. Nous allons en donner une formulation fondée sur le principe des travaux virtuels.

Soit 行 le volume occupé par le solide au repos, 臨 sa frontière. Supposons que sur une partie 臨⁰ de 臨 le solide soit fixé et que sur le reste 臨¹ on lui applique une force de densité superficielle g . Un déplacement admissible est un champ de vecteurs qui s’annule sur 臨⁰. Soit u (x ) le déplacement du point du solide qui se trouve en x au repos. On sait que chaque composante de la densité des forces élastiques s’écrit:

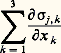靖 est le tenseur des contraintes, qui est symétrique. Leur travail dans un déplacement virtuel admissible v est:

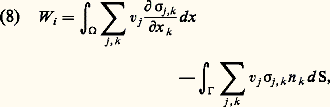où l’indice i évoque le mot «interne»; les n ^k sont les composantes de la normale sortante et d S la mesure superficielle sur 臨. Soit directement par des considérations physiques qu’il serait trop long de décrire ici, soit en appliquant à (8) une intégration par parties et en tenant compte de la symétrie de 靖, on arrive à la nouvelle formule:

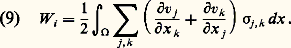La loi de comportement donne l’expression de 靖 qui dépend des dérivées de u et (si le solide étudié est inhomogène) de x . Usuellement, si la déformation est assez petite pour que le solide reste élastique, il suffit de supposer la dépendance en u linéaire. Mais il est important de comprendre que nous n’avons pas besoin de cette simplification ici; nous ne la faisons donc pas.

Avant d’écrire que le travail virtuel des forces élastiques est égal à celui de la force appliquée, à préciser ce qu’est un déplacement admissible. Il faut qu’il satisfasse aux liaisons imposées au système, c’est-à-dire ici qu’il s’annule sur 臨⁰. Il faut de plus qu’il vérifie une condition de régularité qui assure au minimum l’existence de l’intégrale qui figure dans la formule (9), nous y reviendrons. On aboutit à la formulation variationnelle du problème de la recherche du déplacement à l’équilibre: Trouver un déplacement admissible u qui vérifie pour tout déplacement admissible v:

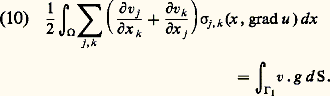En généralisant un peu, on arrive à la formulation suivante, où V est un espace de fonctions sur 行 (qui peuvent être à valeurs vectorielles) et les Fⁱ des fonctions connues (il est commode et peu restrictif de supposer qu’elles vérifient Fⁱ (x , 0, 0) = 0): «Trouver u appartenant à V telle que pour toute fonction v appartenant à V:

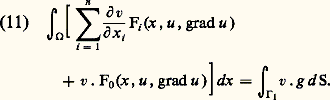Des intégrations par parties montrent que u vérifie l’équation aux dérivées partielles du second ordre:

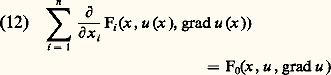et des conditions aux limites qui dépendent du choix de l’espace V.

Le plus grand avantage des formulations variationnelles est justement de contenir à la fois l’équation aux dérivées partielles et les conditions aux limites. Voyons cela de plus près pour les problèmes mêlés. Sous forme classique, nous cherchons u deux fois différentiable qui vérifie (6) sur 行, u = g ⁰ sur 臨⁰ et 煉ⁿ u = g ¹ sur 臨¹, où g ⁰ et g ¹ sont des fonctions données. C’est la formule de Green qui va nous permettre de passer à la forme variationnelle. Elle assure que pour toute fonction v suffisamment régulière et nulle sur 臨⁰:

Il reste à définir l’espace V. Débarrassons-nous d’abord d’un détail: une fonction appartenant à V devra s’annuler sur 臨⁰ alors que la solution u y vaut g ⁰; il faudra en tenir compte dans la formulation du problème. En dehors de cela, il nous reste seulement à préciser quelle condition de régularité doit vérifier une fonction nulle sur 臨⁰ pour appartenir à V. La condition (13) suggère de demander que son gradient ainsi qu’elle-même soient de carré intégrable. Or, c’est exactement la condition que dicte la physique. Dans les applications les plus usuelles, l’expression:

appelée intégrale de Dirichlet , est à un coefficient près l’énergie du système étudié. C’est le cas en élasticité, en électrostatique, dans l’écoulement irrotationnel d’un liquide. L’ensemble des fonctions qui sont de carré intégrable, ainsi que leur gradient, a reçu le nom d’espace de Sobolev et on lui a attribué la notation H¹( 行) (il y a des espaces de Sobolev plus généraux). V sera donc l’ensemble des fonctions qui appartiennent à H¹( 行) et s’annulent sur 臨⁰ (un théorème assure que cette dernière condition a bien un sens pour les fonctions appartenant à l’espace de Sobolev). On arrive finalement à la formulation suivante: «Trouver u 捻 H¹( 行) telle que sa restriction à 臨⁰ soit g ⁰ et que, pour tout v 捻 V, la relation (13) soit vérifiée.»

On notera que les conditions de Dirichlet et de Neumann ont des statuts très différents dans la formulation variationnelle: la première doit être imposée à u et aussi, par l’intermédiaire de la définition de V, à v, alors que la seconde est intégrée dans la relation (10), (11) ou (13) selon le cas.

La monotonie

Le fait d’admettre une formulation variationnelle du type (11) n’implique pas qu’une équation ou un système soit elliptique. Au demeurant, les méthodes d’étude liées à la formulation variationnelle admettent une extension au cas hyperbolique, c’est ce qu’on appelle la méthode des inégalités d’énergie . Ce qui caractérise l’ellipticité, c’est une propriété des fonctions Fⁱ que nous allons aborder maintenant.

Les propriétés des solutions d’une équation aux dérivées partielles sont surtout déterminées par les termes contenant les dérivées de l’ordre le plus élevé (ici 2). Nous allons donc concentrer notre attention sur la dépendance en grad u des fonctions Fⁱ de la formule (11). Nous supposerons que ⁰ = 0, comme c’est d’ailleurs le cas dans l’équation de Poisson-Laplace et dans les équations de l’élasticité, entre autres. Enfin, nous examinons le cas d’une équation, le passage à un système n’implique pas ici d’idée nouvelle, seulement une complication du formalisme. Nous posons F = (F¹, ..., Fⁿ ).

On dit qu’une fonction F est monotone si pour tout couple (u , v

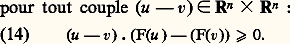Cette terminologie est d’ailleurs assez malheureuse, puisque dans le cas d’une seule variable réelle elle amène à dire qu’une fonction croissante est monotone mais qu’une fonction décroissante ne l’est pas! Il reste qu’elle est adoptée par tous les spécialistes. On dit que la fonction est strictement monotone si le seul cas d’égalité dans (14) est celui où u = v.

Si F est linéaire par rapport à grad u , on peut écrire:

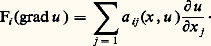La condition de monotonie signifie alors que la partie symétrique de la matrice des a ^ij est positive, et définie positive s’il y a monotonie stricte. On notera en particulier que dans le cas de l’équation de Poisson-Laplace c’est l’opérateur 漣 qui a la propriété de monotonie.

Montrons que si F est strictement monotone, deux solutions du problème variationnel ne peuvent différer que par l’addition d’une constante. Soient u ¹ et u ² ces deux solutions. Écrivons la relation variationnelle (11) pour chacune des deux avec la même fonction v = u ¹ 漣 u ², puis retranchons l’une à l’autre les deux équations obtenues. Nous aboutissons à:

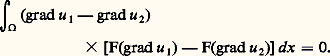Si u ¹ 漣 u ² n’était pas constante, la fonction à intégrer dans le premier membre de cette équation serait positive et non nulle et, par suite, l’intégrale strictement positive.

Si F est strictement monotone, il suffit donc que l’espace V du problème variationnel ne contienne pas de constante non nulle pour qu’il y ait unicité; ce sera le cas si on a imposé la valeur de la solution sur une partie de la frontière. Dans d’autres cas, c’est la présence d’un terme en ⁰ strictement positif qui élimine la constante. Dans d’autres cas encore, tel celui du problème de Neumann, il existe bel et bien toute une famille de solutions différant deux à deux d’une constante.

Avec des conditions d’uniformité de la monotonie et des conditions de continuité assez faibles pour pouvoir être vérifiées dans la plupart des problèmes usuels, on démontre l’existence d’une solution (théorème de Minty-Browder). La démonstration, assez technique, se fait en deux étapes. La première consiste à démontrer l’existence dans le cas de la dimension finie. Elle s’appuie essentiellement sur un résultat de topologie algébrique (le «théorème des antipodes» de Borsuk). La seconde étape consiste à démontrer la convergence des approximations de Ritz-Galerkine que nous décrirons à propos de l’analyse numérique (cf. équations aux DÉRIVÉES PARTIELLES - Analyse numérique).

Formulation variationnelle et calcul des variations

Dans de nombreux problèmes, parmi lesquels les plus fréquents dans les applications, la formulation variationnelle exprime que la solution u est point critique d’une fonctionnelle J sur l’espace V. Ainsi du problème mêlé pour l’équation de Poisson-Laplace (et comme cas particuliers des problèmes de Dirichlet et de Neumann). La fonctionnelle J est dans ce cas définie par la formule:

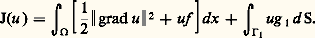Les équations linéaires du second ordre pour lesquelles une telle fonctionnelle peut se trouver sont celles qui s’écrivent:

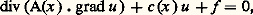où A est une matrice symétrique.

Lorsque cette fonctionnelle existe, on est donc ramené à un problème d’optimisation. La propriété de monotonie équivaut à la convexité de la fonctionnelle, qu’il s’agit donc de minimiser. Ce point de vue est développé dans l’article OPTIMISATION ET CONTRÔLE où on trouvera par la même occasion des indications sur les inéquations.

La fonctionnelle J a souvent une interprétation comme énergie potentielle du système. Sa convexité indique donc la stabilité de la configuration d’équilibre, elle lui est même équivalente dans le cas linéaire. Dans les formulations variationnelles, l’absence de fonctionnelle correspond souvent à une non-conservation de l’énergie, la condition de monotonie indiquant qu’il y a dissipation.

3. L’équation de la chaleur et le type parabolique

Si les équations hyperboliques décrivent l’évolution des phénomènes physiques réversibles, les phénomènes irréversibles relèvent du type parabolique dont le prototype est l’équation de la chaleur, dite aussi de Fourier:

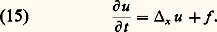Notons tout de suite qu’au contraire de l’équation des ondes cette équation est modifiée par le changement de t en 漣 t .

Elle décrit la diffusion de la chaleur, mais aussi bien d’autres phénomènes de diffusion, en particulier celle d’un corps en solution.

Les problèmes bien posés typiques de l’équation de la chaleur, et des équations paraboliques en général, sont des problèmes mixtes . On donne un ouvert 行 de l’espace et on cherche une solution u sur [0, 秊[ 憐 行 qui vérifie une condition initiale : u (0, x ) = u ⁰(x ), u ⁰ fonction donnée et, à chaque instant t , une condition sur la frontière, condition de Dirichlet, ou de Neumann ou mêlée, d’autres parfois. La différence avec le cas hyperbolique est à chercher dans le comportement vis-à-vis de la variable temps. D’abord on ne donne ici que la valeur initiale de u et pas celle de sa dérivée. Ensuite, et c’est le plus important, la solution n’existe en général que dans le futur, c’est-à-dire pour les valeurs positives de t . On retrouve là l’opposition réversibilité-irréversibilité. La coexistence de données initiales et de données à la frontière d’un ouvert d’espace n’est pas essentielle: on la trouve aussi dans certains problèmes hyperboliques.

Certaines propriétés de l’équation de la chaleur la rapprochent de l’équation de Laplace. Supposons pour le moment que f = 0 (c’est-à-dire qu’il n’y a ni source ni absorption de chaleur). Les solutions sont alors indéfiniment différentiables et, lorsqu’on fixe t , ce sont des fonctions analytiques de x . En particulier, la diffusion est instantanée dans ce sens que si dans un problème mixte la donnée initiale est nulle en dehors d’un voisinage d’un point, dès que t est strictement positif, il n’y a plus aucun point au voisinage duquel la solution reste nulle. Ce résultat peut aussi se déduire d’une version du principe du maximum adaptée à l’équation de la chaleur.

Nous allons établir l’équation de la chaleur par un raisonnement qui, convenablement modifié, s’étend aux autres phénomènes de diffusion. Nous prendrons pour u la densité de l’énergie interne, f est celle des sources d’énergie thermique. Nous négligeons les effets dus à la dilatation thermique, autrement nous n’arriverions pas à (15) mais à un système où figurerait cette équation et celles de l’élasticité, le tout modifié par un couplage de ces équations entre elles. Nous désignerons par v le flux d’énergie thermique. Le bilan d’énergie dans un domaine U nous donne ainsi:

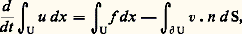où 煉U désigne la frontière de U. Nous transformons une fois de plus l’intégrale de surface en intégrale de volume par une intégration par parties; faisons passer la dérivation par rapport au temps sous le signe d’intégration (u peut-être supposée assez régulière pour que nous en ayons le droit) et obtenons:

Comme cette équation doit être vraie pour tout domaine U, on en déduit: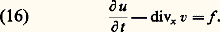

C’est l’équation de continuité dont la validité est extrêmement générale: elle exprime simplement une loi de conservation quelconque.

Il faut maintenant une relation entre u et v. C’est la loi de diffusion proprement dite qu’on prend de la forme:

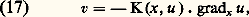où K est a priori une matrice. Les physiciens démontrent qu’elle est symétrique. Elle est définie positive: cette propriété exprime que l’énergie thermique diffuse des régions les plus chaudes vers les plus froides et pas l’inverse. Dans un milieu isotrope, c’est simplement le produit par un nombre. Si le milieu est homogène elle ne dépend pas de x . Pour aboutir à l’équation (15) on suppose toutes ces propriétés vérifiées et on fait de plus l’hypothèse que K ne dépend pas non plus de u , ce qui est une approximation justifiée dans les situations les plus usuelles. Dans tous les cas, (16) et (17) se combinent en:

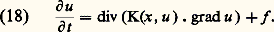Si K est le produit par un nombre constant, un choix adéquat des unités donne la forme (15).

Dans le raisonnement qui précède, on peut remplacer l’énergie interne par la concentration d’une solution sans rien changer d’autre. Des raisonnements analogues s’appliquent aux fluides circulant dans un milieu poreux. Très simples dans le cas d’un liquide saturant les pores, les équations deviennent beaucoup plus compliquées dans le cas d’un gaz ou du mélange de deux fluides.

On notera que (18) peut s’écrire:

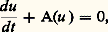où A a la propriété de monotonie. C’est là la clef de propriétés d’existence et d’unicité pour les équations et systèmes paraboliques, sur lesquelles on reviendra dans l’article équations aux DÉRIVÉES PARTIELLES Équations aux dérivées partielles non linéaires.

L’équation de la chaleur et les équations analogues ont un lien étroit avec la théorie des probabilités. On ne s’en étonnera pas puisque la relation (17) repose sur une théorie relevant de la physique statistique.

Pour nous borner à un aspect assez simple de cette question, considérons des solutions de l’équation:

vérifiant une condition de décroissance à l’infini sur Rⁿ (par exemple intégrables). On passe alors de la solution à l’instant t ¹ à la solution à un instant ultérieur t ² par la formule: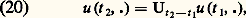

où U^t est l’opérateur d’évolution , défini dans ce cas par la formule:

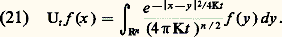Cet opérateur transforme les mesures de probabilités sur Rⁿ en mesures de probabilités sur Rⁿ et les gaussiennes en gaussiennes. C’est donc l’opérateur de transition d’un processus de Markov gaussien.

Réciproquement, on vérifie que tout processus de Markov gaussien à accroissements indépendants et stationnaires, commutant avec les déplacements de l’espace, est donné par les formules (20) et (21).

En plus des équations de diffusion, les systèmes paraboliques comprennent les équations de Navier-Stokes pour un fluide incompressible:

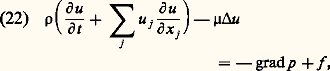où u est la vitesse du liquide, p sa pression, 福 sa densité, 猪 son coefficient de viscosité et f la force extérieure. De plus, on impose à u d’être de divergence nulle: c’est l’équation de continuité.

4. Autres équations

Équations qui changent de type

L’équation de Tricomi:

est hyperbolique dans le demi-plan x ² 麗 0, elliptique dans le demi-plan x ² 礪 0.

En dehors de cela, le principal intérêt de l’équation de Tricomi est sa simplicité qui a permis d’en faire une étude assez détaillée. On rencontre un système présentant le même changement de type dans l’étude des écoulements stationnaires de fluides compressibles non visqueux ^{[cf. AÉRODYNAMIQUE]}. En admettant que l’équation d’état permet d’écrire la pression comme une fonction p de la densité, les équations du mouvement s’écrivent dans ce cas :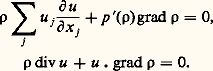

Les notations ont le même sens que dans l’équation (22); p ( 福) est le carré de la vitesse de propagation du son dans le fluide, on voit qu’elle dépend de x par l’intermédiaire de la densité. Dans la région subsonique, c’est-à-dire celle où 瑩u 瑩² 麗 p ( 福), le système est elliptique, il est hyperbolique dans la région supersonique, c’est-à-dire celle où 瑩u 瑩² 礪 p ( 福).

Dans les équations et systèmes hyperboliques dont nous avons parlé jusqu’ici, la variable temps jouait un rôle privilégié; ce rôle est tenu dans la région supersonique par le déplacement dans la direction de l’écoulement. On peut d’ailleurs dans ce cas entendre la propagation des singularités dans la région hyperbolique: c’est le «bang» de l’avion passant le mur du son.

Naturellement, c’est dans les régions comportant à la fois des parties supersoniques et des parties subsoniques que l’étude de l’écoulement est la plus délicate (régions transsoniques, fig. 3). L’étude de ces régions transsoniques connaît un regain d’intérêt car la hausse du prix du carburant a amené à renoncer, pour les avions de ligne du futur, aux vitesses supersoniques.

L’équation de Schrödinger

L’équation de Schrödinger:

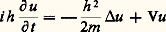décrit en physique quantique l’évolution de la fonction d’onde u d’une particule non relativiste de masse m soumise à un potentiel V. Elle n’est pas hyperbolique, ce qui semble mettre en défaut l’assertion selon laquelle la physique des phénomènes réversibles est décrite par des systèmes hyperboliques. Mais il ne faut pas oublier que l’équation de Schrödinger apparaît comme une approximation à faible vitesse de l’équation de Dirac qui, elle, est un système hyperbolique.

Malgré une certaine ressemblance formelle avec l’équation de la chaleur, elle n’est pas non plus parabolique; le facteur i devant la dérivée par rapport au temps assure la réversibilité.

L’équation de Schrödinger n’appartient finalement pas à un type particulier d’équations. Malgré son importance physique, elle apparaît assez comme un cas particulier – au moins pour le moment.

Dans le même ordre d’idées, l’équation de Korteweg et de Vries et les autres équations «à solitons», dont les propriétés seront exposées dans la partie consacrée aux problèmes non linéaires, ont des caractères analogues: elles ne sont pas hyperboliques mais liées à des équations hyperboliques.

Équations générales

Occupons-nous d’abord des équations aux dérivées partielles linéaires à coefficients constants du second ordre à trois variables indépendantes. Par un changement de variables, on peut toujours se ramener à un des trois cas suivants:

a ) la partie principale (homogène d’ordre deux) de l’équation est incomplète (c’est-à-dire qu’il n’y figure pas de dérivation par rapport à une des variables);

b ) cette partie principale est l’opérateur de Laplace, l’équation est elliptique;

c ) la partie principale est l’opérateur des ondes (à deux dimensions d’espace), l’équation est hyperbolique.

Si on passe à quatre variables indépendantes, un quatrième cas se présente, celui de l’équation:

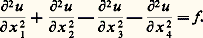Cette équation est appelée ultra-hyperbolique par allusion au fait qu’il y a un signe de plus que dans l’équation des ondes. Mais cette expression ne désigne pas un type comme l’hyperbolique ou le parabolique; c’est au fond une désignation purement négative. Elle ne correspond ni à des propriétés de problèmes bien posés ou à des singularités de solutions, ni à une famille qu’on saurait caractériser sur la forme de l’équation, y compris pour les ordres supérieurs à deux.

Au demeurant, cette équation n’intervient pas dans des problèmes physiques.

En principe, la théorie de Sato, Kashiwara et Kawai doit permettre une classification des systèmes linéaires aux dérivées partielles (cf. équations aux DÉRIVÉES PARTIELLES Analyse microlocale). Malheureusement, elle est d’un caractère tellement abstrait et détourné qu’on n’a encore guère vu d’application à un cas particulier non classique.

Encyclopédie Universelle. 2012.